گزارش ارقام اندازه‌گیری شده در شیمی بسیار حائز اهمیت است و شما بایستی قادر باشید کمیت‌های مختلف را به صورت تجربی در آزمایشگاه اندازه‌گیری کرده و نتایج را به صورت صحیح گزارش دهید. برای این منظور لازم است با مفاهیم قطعیت و عدم قطعیت آشنا باشید و همچنین از تخمین برای گزارش داده‌ها استفاده کنید. آشنایی با ارقام بامعنا و حفظ دقت و قطعیت در انجام محاسبات ریاضی که ممکن است بر روی مقادیر اندازه گیری شده اعمال گردد نیز ضروری است.
در ادامه با این مفاهیم و مثالهای مختلف در این زمینه آشنا خواهید شد.
قطعیت و عدم قطعیت اندازه‌گیری در شیمی
قطعیت اندازه گیری در واقع نشان دهنده میزان دقت اندازه گیری است برای درک بهتر مثال زیر را در نظر بگیرید:
گاز مونوکسید کربن گازی بی رنگ است که توسط وسایل نقلیه موتوری موتوری منتشر می‌شود و یکی از عوامل آلودگی هوا است. در جدول 1 و جدول 2 ، دو گزارش از غلظت مونوکسید کربن در سالهای 1990 تا 2017 در یکی از شهرهای آمریکا را مشاهده می‌کنید.
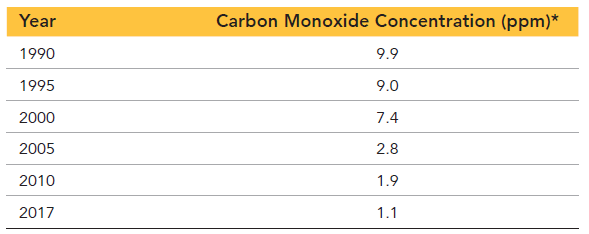
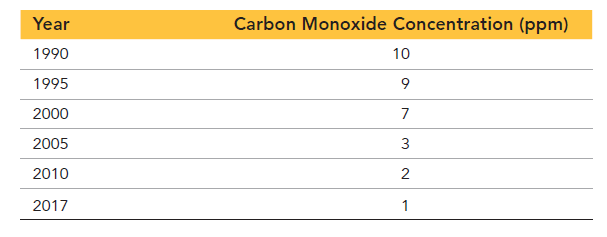
از مقایسه این دو جدول، به دو نکته قابل توجه پی می‌برید. اول اینکه با گذشت زمان، غلظت زمان غلظت مونوکسید کربن هوا کاهش یافته است که احتمالا به خاطر استفاده از موتورهای کارآمدتر، سوخت‌های بهتر و اصلاحات انجام گرفته جهت دستیابی به هوای پاک است.
دوم اینکه تعداد ارقامی است که اندازه‌گیری‌ها با آن گزارش شده‌اند. مجموعه اول با دقت 0.1ppm گزارش شده است ولی مجموعه دوم با دقت 1ppm گزارش شده است. در واقع تعداد ارقام در یک اندازه گیری، میزان قطعیت مرتبط با آن اندازه‌گیری را نشان می‌دهد. هر چقدر ارقام بیشتر، قطعیت بیشتر و هر چقدر ارقام کمتر باشد، قطعیت کمتر است. بنابراین قطعیت داده‌های جدول 1 بیشتر از داده‌های جدول 2 است.
بنابراین در کنار قطعیت داده های گزارش شده، یک عدم قطعیت هم وجود دارد که نشان دهنده سطح اطمینان از اعداد گزارش شده است. دقت داشته باشید که معمولا اعداد طوری نوشته می‌شوند که عدم قطعیت در آخرین رقم گزارش شده گزارش شود و میزان آن هم به اندازه 1 واحد است (مگر اینکه خلاف آن ذکر شده باشد). به عنوان مثال وقتی که غلظت کربن مونوکسید در سال 2010 با مقدار 1.9ppm ذکر شده است. به این معنا است که دقت اندازه‌گیری آن برابر 0.1ppm بوده و نشان دهنده این است که غلظت مونوکسید کربن بین 1.8ppm تا 2.0ppm قرار دارد.
ولی در مجموعه دوم که مقدار گزارش شده برابر 2ppm است، به این معنا است که غلظت مونوکسید کربن بین 1ppm تا 3ppm قرار دارد.
به طور کلی اندازه‌گیری‌های علمی به گونه‌ای گزارش می‌شوند که تمام ارقام قطعی هستند به جز رقم آخر که تخمینی است.
برای مثال، عدد گزارش شده زیر را در نظر بگیرید:
سه رقم اول قطعی هستند ولی رقم آخر تخمینی است.
نحوه گزارش ارقام اندازه‌گیری شده در شیمی
تعداد ارقام گزارش شده در یک اندازه‌گیری به دستگاه اندازه‌گیری بستگی دارد. وزن کردن یک دانه پسته را با دو ترازوی مختلف در نظر بگیرید که در شکل زیر نمایش داده شده است.
در ترازوی بالایی هر 1 گرم دارای علامت گذاری است، در حالی که ترازوی پایینی هر 0.1 گرم علامت دارد. در ترازوی بالایی عقربه بین 1 و 2 گرم قرار دارد، فضای بین علامت‌های 1 و 2 گرمی را به ده فضای مساوی تقسیم می‌کنیم و تخمین می‌زنیم که عقربه حدود 1.2 گرم است. سپس اندازه‌گیری را 1.2 گرم می‌نویسیم، که نشان می‌دهد از “1” مطمئن هستیم اما “0.2” را تخمین زده‌ایم.
ترازوی پایینی، با علامت‌هایی هر دهم گرم، مستلزم آن است که نتیجه را با ارقام بیشتری بنویسیم. عقربه بین علامت 1.2 گرم و علامت 1.3 گرم قرار دارد. دوباره فضای بین دو علامت را به ده فضای مساوی تقسیم می‌کنیم و رقم سوم را تخمین می‌زنیم. برای شکل نشان داده شده، 1.27 گرم گزارش می‌دهیم.
نحوه گزارش حجم مایع با استفاده از استوانه مدرج
استوانه مدرج نشان داده شده در شکل زیر را در نظر بگیرید، هر 0.1 میلی‌لیتر دارای علامت‌گذاری است. حجم (پایین ترین قسمت انحنای مایع) را بایستی با تعداد صحیح ارقام گزارش کنید.
از آنجایی که پایین ترین قسمت انحنای مایع بین علامت‌های ۴.۵ و ۴.۶ میلی‌لیتر است، فضای بین علامت‌ها را به صورت ذهنی به ده فضای مساوی تقسیم کنید و رقم بعدی را تخمین بزنید. در این حالت، باید نتیجه را ۴.۵۷ میلی‌لیتر گزارش کنید. اگر کمی متفاوت تخمین زده باشید و ۴.۵۶ میلی‌لیتر نوشته باشید، چه می‌شود؟ به طور کلی، اختلاف یک واحدی در رقم آخر قابل قبول است زیرا رقم آخر تخمین زده می‌شود و افراد مختلف ممکن است آن را کمی متفاوت تخمین بزنند. با این حال، اگر ۴.۶۳ میلی‌لیتر نوشته باشید، اندازه‌گیری را اشتباه گزارش کرده‌اید.
به عنوان تمرین دمای دماسنج نشان داده شده در پایین شکل بالا را با تعداد صحیح ارقام ثبت کنید.
قطعیت و عدم قطعیت و نحوه گزارش ارقام اندازه‌گیری شده در شیمی
ارقام معنادار
دقت اندازه گیری که بستگی به دستگاه مورد اندازه گیری دارد، بایستی در حین اندازه گیری و همچنین محاسبات مرتبط با آن اندازه گیری حفظ گردد. برای این منظور از ارقام معنا دار استفاده می‌کنیم. در هر اندازه گیری که گزارش می‌کنیم، ارقامی که مشخص کننده مکان اعشار نباشند، به عنوان ارقام معنادار شناخته می‌شوند. هر چه تعداد ارقام بامعنا بیشتر باشد، قطعیت اندازه گیری بیشتر است. به عنوان مثال، عدد 23.5 سه رقم معنادار دارد. در حالیکه عدد 23.56 دارای چهار رقم معنا دار است.
ارقام معنا دار در اعداد حاوی صفر
برای تعیین تعداد ارقام معنادار در عددی که حاوی صفر است، بین صفرهایی که معنادار هستند و آن‌هایی که صرفاً رقم اعشار را مشخص می‌کنند، تفاوت قائل می‌شویم.
به عنوان مثال، در عدد ۰.۰۰۰۸، صفرهای ابتدایی (صفرهای سمت چپ اولین رقم غیر صفر) مشخص کننده ارقام اعشاری هستند و تاثیری در قطعیت اندازه گیری ندارند و معنادار نیستند و می‌توان گفت که این عدد فقط یک رقم بامعنی دارد.
ولی صفرهای انتهایی (صفرهای انتهای یک عدد) در عدد ۰.۰۰۰۸۰۰ قطعیت اندازه‌گیری را افزایش می دهند و معنادار محسوب می‌شوند و می‌توان گفت که این عدد سه رقم معنادار دارد.
چگونگی شمارش ارقام معنادار
برای شمارش ارقام معنادار بایستی نکات زیر را در نظر بگیرید:
۱. همه ارقام غیر صفر معنادار هستند. مثال:
۲. صفرهای داخلی (صفرهای بین دو رقم غیر صفر) معنادار هستند. مثال:
۳. صفرهای ابتدایی (صفرهای سمت چپ اولین رقم غیر صفر) معنی‌دار نیستند. آنها فقط برای تعیین محل نقطه اعشار استفاده می‌شوند.
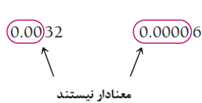
۴. صفرهای انتهایی به صورت زیر طبقه‌بندی می‌شوند:
صفرهای انتهایی بعد از یک نقطه اعشار همیشه معنی‌دار هستند.
صفرهای انتهایی قبل از یک نقطه اعشار (و بعد از یک عدد غیر صفر) همیشه معنی‌دار هستند.
صفرهای انتهایی بدون استفاده از نقطه اعشار مبهم هستند و بایستی در آنها از نمادهای علمی استفاده کرد.
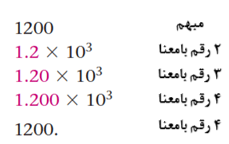
اعداد دقیق
اعداد دقیق هیچ عدم قطعیتی ندارند و محدود کننده تعداد ارقام معنادار در هیچ محاسبه‌ای نیستند. در واقع می‌توانیم یک عدد دقیق را به عنوان عددی در نظر بگیریم که تعداد نامحدودی رقم معنادار دارد.
اعداد دقیق از 3 گروه مختلف نشات می‌گیرند:
- از شمارش دقیق اجسام مجزا. به عنوان مثال، ۳ اتم به معنی ۳.۰۰۰۰۰ اتم است.
- از کمیت‌های تعریف شده، مانند معادل سانتی‌متر یک متر. از آنجا که ۱۰۰ سانتی‌متر به عنوان ۱ متر تعریف می‌شود،
۱۰۰ سانتی‌متر = ۱ متر به معنی ۱۰۰.۰۰۰۰۰ سانتی‌متر = ۱.۰۰۰۰۰ متر است.
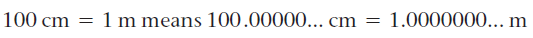
- از اعداد صحیحی که بخشی از یک معادله هستند. برای مثال، در معادله‌ی
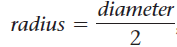
عدد ۲ دقیق است و تعداد نامحدودی رقم معنی‌دار دارد.
محاسبه ارقام معنادار در اعداد مختلف
در جدول زیر تعداد ارقام بامعنا برای ارقام مختلف و نحوه محاسبه آنها آورده شده است.
| عدد | تعداد ارقام معنادار |
| 0.04450m | دارای چهار رقم معنادار است. دو عدد ۴ و ۵ معنادار هستند (قانون ۱). صفر انتهایی نیز بعد از یک نقطه اعشار قرار دارد و بنابراین معنادار است (قانون ۴). صفرهای ابتدایی عدد فقط رقم اعشار را نشان می‌دهند و معنادار نیستند (قانون ۳) |
| 5.0003km | دارای پنج رقم معنادار است. اعداد ۵ و ۳ معنادار هستند (قانون ۱)، همچنین سه صفر داخلی (قانون ۲) نیز معنادار هستند. |
| 1dm=10m | دارای بی نهایت رقم معنادار است. کمیت‌های تعریف‌شده دارای تعداد نامحدودی رقم بامعنی هستند. |
| 105*1.000 | دارای چهار رقم معنادار است. عدد ۱ معنادار است (قانون ۱). صفرهای بعدی نیز بعد از یک نقطه اعشار قرار دارند و معنی‌دار هستند (قانون ۴). |
| 0.00002mm | دارای یک رقم معنادار است. عدد ۲ معنادار است (قانون ۱) و صفرهای ابتدایی فقط رقم اعشار را مشخص می‌کنند و بنابراین معنادار نیستند (قانون ۳). |
| 10000m | دارای ارقام معنادار مبهم است . عدد ۱ معنادار است (قانون ۱) و صفرهای انتهایی بدون حضور نقطه اعشاری هستند و مبهم در نظر گرفته می‌شوند (قانون ۴).بهتر است این عدد به صورت 1*105 نوشته شود تا یک رقم معنی‌دار را نشان دهد یا به صورت 1.0000*105نوشته شود تا پنج رقم معنی‌دار را نشان دهد (قانون ۴). |
ارقام معنا دار در محاسبات ریاضی
وقتی که محاسباتی را بر روی کمیت‌های اندازه گیری شده انجام می‌دهیم، نتایج بدست آمده بایستی منعکس کننده دقت کمیت اندازه گیری شده باشند و در طی عملیات ریاضی نباید دقت اندازه گیری افزایش یا کاهش یابد.
بنابراین در طی انجام محاسبات ریاضی بر روی کمیت‌های اندازه گیری شده، رعایت نکات زیر ضروری است:
1) در عملیات ریاضی ضری و تقسیم، تعداد ارقام بامعنای حاصله، برابر تعداد ارقام عامل دارای کمترین رقم بامعنا است.
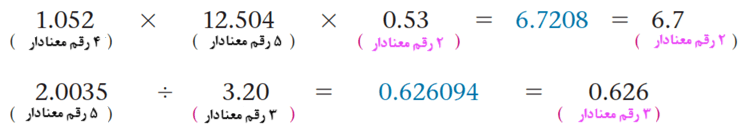
2) در عملیات ریاصی جمع یا تفریق، تعداد ارقام اعشاری حاصله برابر با تعداد رقم اعشار کمیت دارای کمترین رقم اعشار است.
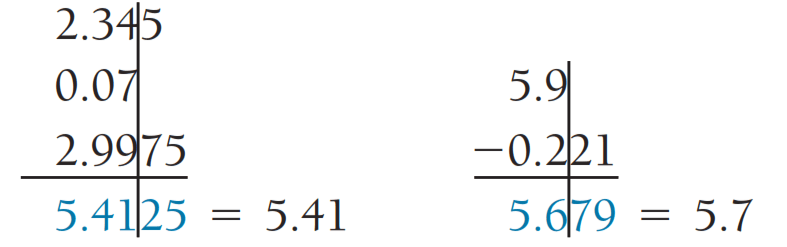
3)هنگام کرد کردن ارقام معنادار به مقادیر صحیح: اگر آخرین رقم چهار یا کمتر باشد به سمت پایین گرد کنید و اگر آخرین رقم پنج یا بیشتر باشد به سمت بالا گرد می‌شود.
4) به منظور کاهش خطاهای گرد کردن در محاسبات چند مرحله‌ای فقط جواب نهایی را گرد کنید.
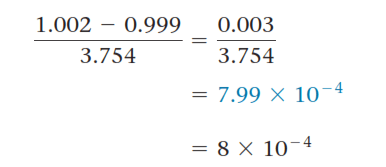
توجه داشته باشید که در ضرب یا تقسیم، کمیتی که کمترین رقم معنی‌دار را دارد، تعداد ارقام معنادار در پاسخ را تعیین می‌کند، اما در جمع و تفریق، کمیتی که کمترین رقم اعشار را دارد، تعداد رقم‌های اعشار در پاسخ را تعیین می‌کند.
در ضرب و تقسیم، ما روی ارقام معنادار اما در جمع و تفریق روی ارقام اعشاری تمرکز می‌کنیم. وقتی مسئله‌ای شامل جمع یا تفریق باشد، ممکن است تعداد ارقام معنادار پاسخ با تعداد ارقام اولیه متفاوت باشد. این نکته را در مسائلی که شامل جمع یا تفریق و ضرب یا تقسیم می‌شوند، در نظر داشته باشید. برای مثال،
جواب فقط یک رقم معنی‌دار دارد، علی رغم اینکه اعداد اولیه سه یا چهار رقم معنی‌دار دارند.
صحت و دقت اندازه گیری
دانشمندان اغلب اندازه‌گیری‌ها را چندین بار تکرار می‌کنند تا از نتایج اطمینان یابند. ما در اندازه گیری ها با دو نوع قطعیت مواجه هستیم: صحت و دقت اندازه‌گیری.
صحت اندازه‌گیری به این معنی است که مقدار اندازه‌گیری شده چقدر به مقدار واقعی نزدیک است. دقت به این اشاره دارد که یک سری اندازه‌گیری چقدر به یکدیگر نزدیک بوده و قابل تکرار می‌باشند. برخی اندازه‌گیری ها می‌توانند دقیق باشند (از نظر اینکه مقادیر چقدر به یکدیگر نزدیک بوده و قابل تکرار هستند) ولی صحت نداشته باشند (به مقدار واقعی نزدیک نباشند). نتایج به دست آمده توسط سه دانشجو را در نظر بگیرید که چندین بار یک بلوک سربی را که وزن واقعی آن 10.00 گرم است (با خط آبی افقی ممتد روی نمودارهای شکل زیر نشان داده شده است) وزن کردند.
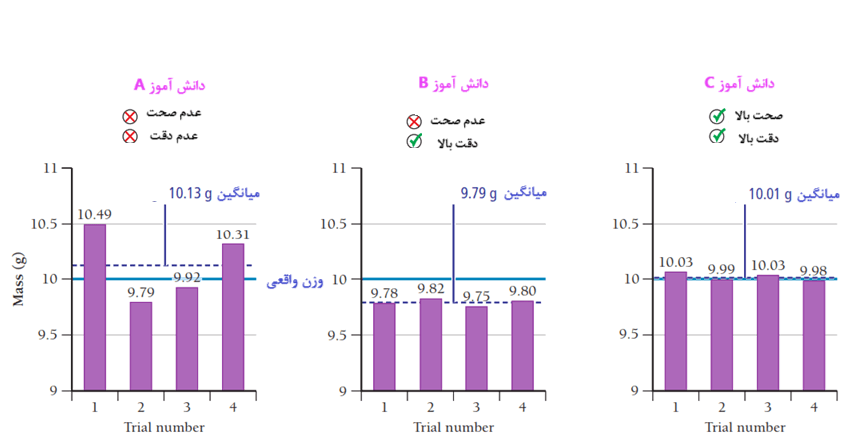
نتایج دانشجوی A هم صحت ندارند (به مقدار واقعی نزدیک نیست) و هم دقیق (اعداد بهم نزدیک نیستند) نیستند. این ناسازگاری نتیجه خطای تصادفی است. تقریباً همه اندازه‌گیری‌ها دارای درجه‌ای از خطای تصادفی هستند و می‌توان آن را با آزمایش‌های بیشتر به حد میانگین رساند.
نتایج دانشجوی B دقیق اما نادرست است. این عدم دقت نتیجه خطای سیستماتیک است. برخلاف خطای تصادفی، خطای سیستماتیک با آزمایش‌های مکرر به میانگین نمی‌رسد. به عنوان مثال اگر یک ترازو به درستی کالیبره نشده باشد، به طور سیستماتیک اوزان را بالاتر یا پایین تر از مقدار صحیح نشان می‌دهد.
نتایج دانشجوی C خطای سیستماتیک یا خطای تصادفی کمی را نشان می‌دهد و می توان نتایج اندازه گیری وی را هم دقیق و هم صحیح درنظر گرفت.
نتیجه‌گیری
در این مقاله با مفاهیم قطعیت، عدم قطعیت، دقت و صحت اندازه‌گیری و نحوه استفاده از این مفاهیم در بررسی داده های اندازه گیری شده مختلف آشنا شدید و آموختید که در اندازه‌گیری هایی که به طور تجربی انجام می‌دهید، چگونه به صورت صحیح از تخمین برای گزارش صحیح داده‌ها استفاده کنید. همچنین با مفهوم ارقام بامعنا و لزوم حفظ دقت اندازه گیری در طی محاسبات ریاضی آشنا شدید و برای درک بهتر مثالهایی در این زمینه ارائه گردید. اگر سوالی برای شما پیش آمده و یا نکته نظری داشتید، حتما در بخش دیدگاهها با ما در میان بگذارید.
مراجع
Oxtoby, D.W., Gillis, H.P. and Butler, L.J., 2016. Principles of modern chemistry. Cengage AU.
